| preface
|| intro || 1
|| 2 || 3
|| 4 || 5
|| 6 || 7
|| 8 || 9
|| 10 || Epil
|| Biblio
Foundations
of Philosophy
2
Identifying Direct Insights
Intelligence and intelligibility are the obverse and reverse
of the second level of knowing: intelligence looks for intelligible patterns in
presentations and representations; it grasps such patterns in its moments of
insight; it exploits such grasp in its formulations and in further operations
equally guided by insights.1
Preliminary Exercises.
(1) Move only three of the eight sticks and reverse the
direction of the fish.
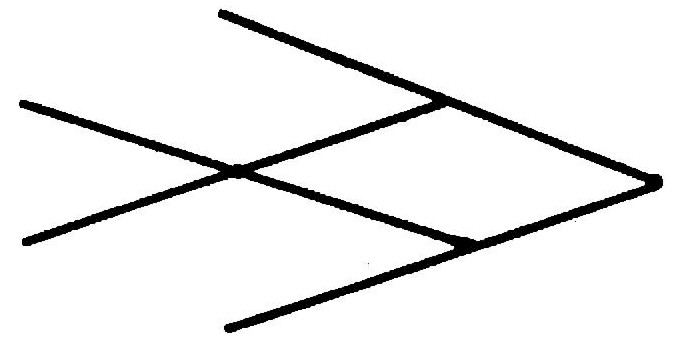
(2) Join all nine points using only four straight lines which
must be drawn continuously - without lifting the pen and without retracing your
steps. [58]
.
. .
.
. .
.
. .
(3) Given that D = 5 what are the values of the other
letters in this addition sum:
D O N A L D
G E R A L D
R O B E R T
(4) Give the next number in the following sequences:
(a) 5, 15, 25, …..
(b) 7, 3, -1, …..
(c) 1, -2, 4, -8, …..
(d) 1, 7, 25, …..
(5) Are you looking at this box from above or from below?

(6) Identify and describe an insight that you have had
recently.
1. The Experience of Insight
In 1993 Nigel Short qualified to play Gary Kasparov, the
reigning World Chess champion, for the World Title. As the games were in London
and Nigel was a local boy, the BBC decided to televise the series live. As chess
does not present much visible action, they assembled a team of commentators and
analysts to fill in the gaps. However, during the sixth game Kasparov spent
fifty-five minutes thinking about one move: almost an hour, motionless,
transfixed, impassive, staring at the board, uttering an occasional sigh.
Commentators soon ran out of chatter and the chess experts [59] exhausted their
analysis. Still no move. BBC does not have commercial breaks, so you could feel
the tension rising. Finally, one of the commentators cries out in exasperation,
What on earth is he doing?
That is precisely our question also in this chapter: what is
thinking? What are we doing when we are thinking? Why does it take so long? What
brings it to an end? What kinds of activities are involved in understanding? It
is clear that it takes time: fifty-five minutes to be precise in this case. It
is clear that it is an activity: Kasparov was not asleep, he was not relaxing,
nor daydreaming. There is a limit to the time allowed; he wanted desperately to
win; he had to use his time wisely. It is not a visible activity that you can
catch on a television camera but it is an activity which we can describe,
analyze, define, break into its parts and put them together again as a whole.
That is what we will be doing in this chapter.
What was Kasparov doing for those fifty-five minutes? Well,
he was thinking; he was considering possibilities, analyzing three or four main
lines to a depth of six or ten moves, involving hundreds of possible end
positions. He was using his imagination to picture the board with pieces
removed or advanced; he was using his memory to call up similar games and
situations; above all he was using his intelligence to relate, combine,
put together sequences of possible moves and corresponding replies; he was being
systematic, eliminating this line, exploring alternatives, looking at the
situation from his point of view and that of his opponent. He was evaluating
positions, advantages, material loss, attacking possibilities, balancing tactics
and strategy. Finally, the whole movement coalesces into the judgment: this is
the best move. Much to the relief of the commentators he moved a piece. The game
ended in a draw but he won the series.
Our interest in Kasparov, chess, and what he was doing is
marginal. Our primary focus is our own modest efforts to think things through,
to understand correctly, to find correct solutions to problems. The exercises
given at the beginning of the chapter are designed to provoke a simple insight.2
The main purpose of doing the problems is to reflect back afterwards and to
identify the experience of an act of understanding and the factors which help or
[60] hinder understanding to occur. We are not primarily interested in the
content, whether it is chess or mathematics or practical problems; we are
vitally interested in the activity or activities involved in the process. We are
not interested in the what is being understood; we are interested in the
activities by which something is being understood. We are starting the
work of intellectual self-appropriation, taking it step by step, slowly
assembling all the pieces, until finally we will be able to identify and
discriminate with ease our own cognitional operations.
Direct insights are simply acts of understanding; we call
them ‘direct’ to differentiate them from inverse and reflective insights,
which we consider later. Direct insights are the normal, straightforward acts of
understanding involved in working out a chess problem, a mathematics question or
a puzzle. Thinking normally involves a series of insights, a series of
connections, relations, and possibilities. Thinking is like a conversation that
we conduct within ourselves, considering, rejecting, arguing, referring to
examples, invoking images, working things out. Sometimes we reach a solution;
sometimes we remain frustrated.
We are now discussing the intellectual pattern of experience
and so we can expect to discern a pattern of related activities that form some
kind of a unity. At first there is puzzlement even in grasping what is the
problem. What are the elements to be solved? What is the question? What has to
be taken into account? It is tantalizing; it is a challenge to one's
intelligence. If it is a game, there can be considerable aggression, a will to
win, pride, fear and other emotions involved. If it is work, research, a
practical problem, then all sorts of other factors motivate us to solve it. But
in that first stage of puzzlement, we cannot see the solution; we can get very
annoyed at the author or the teacher or the opponent, who has confronted us with
such a challenge.
The next moment everything falls into place; you ‘see’
the solution. It is like a light going on in your mind. It is a release of
tension, a spurt of adrenaline, something clicks. You 'see' what is relevant and
what is irrelevant; you breathe a sigh of relief; you feel confident. The pieces
on the chessboard remain the same, but you 'see' how they relate in a different
way. You 'see' something that [61] you did not see before, even though it was
staring you in the face. We use a variety of metaphors to express this
experience. To ‘see’ is the most common but we also use the expressions, ‘to
grasp the point’, ‘to get it ‘, ‘it dawned on me’, an ‘aha’
experience, a ‘eureka’ experience. These are merely metaphors, that is,
loose ways of using what is familiar to talk about what is difficult less
familiar.
The person of intelligence is the one in whom these acts
occur easily, frequently and with regard to a variety of subjects. We are not
geniuses, but we are all blessed with a minimum of intelligence and are
performing acts of understanding all the time. The not-so-bright person is one
who has difficulty understanding; it takes a longer time, and happens less
frequently. We all know people who are very quick to catch on, to get the point,
to grasp the essential. Others are dull, susceptible to having their legs
pulled; we describe them as slow, dense, thick. The intelligent person learns
faster, concentrates better, absorbs material easily, and gets ahead in his
subject.
We are performing acts of understanding all our waking life;
but for the most part we take them for granted. When we are reading, we are
performing a complicated series of acts of understanding the letters, the words,
the sentences, and the meanings. When we are involved in practical work we using
means to achieve ends, applying the law of the lever, exploiting the principles
of mass and momentum etc. The difficulty is to be able to isolate the experience
of a single act of understanding so that we can describe it, identify it, and
pick out its salient characteristics. The purpose of this chapter is to make a
start in identifying this experience of insight in our own minds. Later we will
be able to expand on the implications of this for understanding, generalization,
abstraction and other processes.
Just a cautionary note on what insight is not. It is not an
intuition; it is not a direct, single, simple vision of intelligible objects.
Understanding involves is a series of related activities, all of which are part
of the process of having an insight. Think of what was going on in the mind of
Kasparov for those fifty-five minutes; why did it take so long? What was he
doing?
Insight is not in itself a religious experience. Religious
experiences can be very dramatic, overwhelming, conversion experiences; such
experiences may involve activities of [62] understanding, a change of world view
or of concepts, but of themselves they primarily refer to God, prayer, behavior,
choice, etc. There is nothing mystical or esoteric about acts of understanding
in themselves; they are very common place; we are performing them all the time.
Finally, insight is not just remembering. We can wander
around for hours looking for our spectacles - especially when we are old.
Suddenly, we remember that we left them in the garden. It comes suddenly and
unexpectedly but it is not an insight. This is simply an act of remembering at
the level of sense.
2. Examples from History
Fortunately, history provides us with many examples of acts
of understanding. Let us take some dramatic, clear cases to see if they can help
us to analyze and identify the activities involved in understanding. Although
they are experiences of historical figures our questions is always, does this
resonate in your own experience?
1. Archimedes, a Greek mathematician, was given a
problem by Hiero, the king. The king had received a chalice of gold, which was
beautifully decorated, from a visiting dignitary. The king wanted to know
whether the chalice was made of pure gold or whether it was mixed with lead. He
asked Archimedes to find out, without melting down the chalice. Archimedes knew
that lead is heavier than gold. He could easily find out the weight of the
chalice but he still had not enough information to work out how much lead and
how much gold. We are told that he tired of the problem and decided to relax and
go to the public baths. Floating in the water, perhaps wondering why he was
floating, he suddenly realized that if he weighed the chalice in water he would
get the further information he needed to solve the problem. He ran naked through
the streets of Syracuse, shouting, 'Eureka, Eureka, I have found it, I have
found it.' Later on, in his calmer moments, I suppose, he worked out the
principles of specific weight and displacement, and realized that they could be
applied to all and every material body to determine whether they would float.
2. A more modern example is that cited by the
mathematician H Poincare. This is an insight into mathematics, but we do not
have to understand the mathematics; what we are interested in is the experience
of insight, which he calls illumination and describes quite clearly.
Just at this time, I left Caen where I was
living, to go on a geological excursion under the auspices of the School of
Mines. The incidents of the travel made me forget my mathematical work.
Having reached Coutances, we entered an omnibus to go some place or other.
At the moment when I put my foot on the step, the idea came to me, without
anything in my former thoughts seeming to have paved the way for it, that
the transformations I had used to define the Fuchsian functions were
identical with those of non-Euclidean geometry. I did not verify the idea; I
should not have had time, as, upon taking my seat in the omnibus, I went on
with a conversation already commenced, but I felt a perfect certainty. On my
return to Caen, for conscience sake, I verified the result at my leisure.
Then I turned my attention to the study of some
arithmetical questions apparently without much success and without a
suspicion of any connection with my preceding researches. Disgusted with my
failure, I went to spend a few days at the seaside and thought of something
else. One morning, walking on the bluff, the idea came to me, with just the
same characteristics of brevity, suddenness and immediate certainty, that
the arithmetic transformations of indefinite ternary quadratic forms were
identical with those of non-Euclidean geometry.3
Here again, we have a mathematician faced with a difficult
problem and unable to solve it after much time and effort. So he takes a break,
relaxes, thinks of something else, and goes for a walk. And quite suddenly, in a
flash, the answer comes to him; he understands the solution. Later on, he can
return to his work and iron out the details. This extract recounts two such
experiences where insights occurred not in the midst of work but at a time of
relaxation.
3. Let us look at the well-known story of Helen
Keller (1880-1968). She was afflicted with a disease at the age of eighteen
months, which deprived her of sight and hearing. She grew up a very unruly
child, cut off from the world, helpless and dependent. When she was six years
old her parents hired Annie Sullivan to be her tutor. Annie herself had suffered
from neglect and cruelty in her youth and also experienced partial blindness.
She was trained in the methods of the Perkins school to communicate with the
blind and deaf by tracing the alphabet on the hand and associating these
movements with common objects. She started using this method with Helen but was
not meeting with much success even though Helen did learn to [64] imitate the
movements on the palm of the hand. On March 3rd, 1887, all this changed, as
Helen describes in her autobiography:
We walked down the path to the well-house, attracted by
the fragrance of the honeysuckle with which it was covered. Someone was
drawing water and my teacher placed my hand under the spout. As the cool
stream gushed over one hand she spelled into the other the word w-a-t-e-r,
first slowly, then rapidly. I stood still, my whole attention fixed upon the
motions of her fingers. Suddenly I felt a thought; and somehow the mystery
of language was revealed to me. I knew then that w-a-t-e-r meant the
wonderful cool something that was flowing over my hand. That living word
awakened my soul, gave it light, hope, joy, set it free! There were barriers
still, it is true, but barriers that could in time be swept away.
I left the well-house eager to learn. Everything had a
name, and each name gave birth to a new thought. As we returned to the house
every object which I touched seemed to quiver with life. That was because I
saw everything with the strange, new sight that had come to me........ It
would have been difficult to find a happier child than I was as I lay in my
crib at the close of that eventful day and lived over the joys it had
brought me, and for the first time longed for a new day to come.4
Helen was seven years old when this incident took place. She
had learned almost nothing in those seven years, her mind blocked by her
blindness and deafness. But this is a liberation, a breakthrough. She discovered
naming: things have names, can be referred to, fall into classes, can be
identified and recognized. So we have the paradox of a blind girl who can now
see - 'that strange new sight' - which we are calling insight or the act of
understanding.
4. A more contemporary example is taken from Scientific
American:
In 1951 David A. Huffman and his classmates
in an electrical engineering graduate course on information theory were given
the choice of a term paper or a final exam. For the term paper, Huffman's
professor, Robert M. Fano, had assigned what at first appeared to be a simple
problem. Students were asked to find the most efficient method of representing
numbers, letters or other symbols using a binary code. Besides being a nimble
intellectual exercise, finding such a code would enable information to be
compressed for transmission over a computer network or for storage in a
computer's memory.
Huffman worked on the problem for months, developing a
number of approaches, but none that he could prove to be the most efficient.
Finally, he despaired of ever reaching a solution and decided to start
studying for the final. Just as he was throwing his notes in the garbage, the
solution [65] came to him. "It was the most singular moment of my
life," Huffman says, "There was the absolute lightening of sudden
realization."5
He had been working from the wrong end of the coding tree;
reverse the process and it works. Huffman's code is now one of the basic ideas
of computer science and data communication.
These examples are somewhat dramatic but they do give good
detailed descriptions of the experience of insight. It is an extremely important
moment of transition from not understanding to understanding, from not seeing to
seeing. A psychologist, E. D. Hutchinson, who has studied many examples of
insights, divides the occurrence of an insight into four stages.6
There is a first stage of preparation when the question is posed but despite
great effort nothing seems to happen. A second stage of incubation or retreat
follows when we temporarily give up on finding a solution, relax, turn our mind
to something else to forget our frustration. There is a third stage of insight
when it just happens; we suddenly see, a light comes on, we get the point, we
have a sudden illumination. Finally, there is a stage where we quietly verify,
clarify and apply the insight. These stages can be perceived in all of the above
examples.
However, what is important is not to study the insights of
others but to recognize the same experience in your own intellectual activity.
You may not be able to remember an experience as vivid as that of Helen Keller.
For most of us the experience of insight is routine, taken for granted, not
adverted to. But we are understanding whenever we are reading, speaking,
listening to a lecture, taking notes, driving a car. The exercises at the
beginning of the chapter are designed to make us stop and think; to jolt us out
of a routine; to provoke the experience of puzzlement, of trying different
solutions, being frustrated, and finally finding the correct answer. Our
interest is not in learning mathematics, but in identifying the experience of
understanding. Do some puzzle and, having found the solution, reflect back on
the mental processes involved in solving it. What images did you use? What
figures did you write down? What led you astray? What blocked you from
understanding? What was the clue that helped you to solve it? Where did the
insight come from? Each one of us has privileged access to the working of our
own minds. Shift the focus from the objects on the paper to the activities [66]
of the mind. There we can examine the intimate details of the experience of
insight. The examples we have given are intended as a kind of mirror in which we
can see the workings of our own understanding. The protracted struggle is only
present when we are confronted with difficult problems. But you will usually
find that our insights conform to the pattern of preparation, incubation,
illumination and verification suggested above.
The above historical examples are all acts of discovering
something for the first time; hence it is very dramatic, joyful, memorable. An
educational system cannot afford the time to allow students to discover
everything for themselves. The accumulated discoveries of generations of
scholars are put together systematically and the student has to understand,
remember, digest it all in one semester and repeat it in the exam. In an
educational system the solution is often presented before the problem; learning
loses the joy of insight and discovery and becomes dull and tedious. It is no so
easy to isolate individual acts of understanding in that process of learning.
Perhaps, an educational system which allowed more time for personal research and
discovery would motivate and encourage students in the search for understanding.7
3. Five Characteristics of Insight
To further our objectification of the act of understanding we
will discuss five characteristics of insight.8
Remember that we are not describing something that happens only in the minds of
geniuses, but rather, what is going on in your own mind all the time when you
are understanding.
3.1 Insight comes as a release of the tension of inquiry
Knowing begins in inquiry, in the asking of questions. The
first sign of the emergence of intelligence is the tension of inquiry, the
questioning of experience. We are all familiar with the incessant questioning of
the child. But even as adults we understand in proportion to the strength of our
desire to know. There is a great difference between the student who has a
personal interest in a subject, and one who is there only because he or she has
no choice. It [67] is that interest which motivates, directs attention, sharpens
concentration, and dismisses distractions. An idle curiosity might move us to
attempt a problem, but it may not be strong enough to keep us at it until it is
solved.
Aristotle starts his Metaphysics with the cryptic
statement, 'All men by nature desire understanding.' On that he built his
metaphysics; on that we build our philosophy. We presuppose a deep, strong Eros
of the mind, an inquiring spirit, and a thirst for knowledge. The stronger,
deeper and more intense the desire, the better chance there is that we will
persevere in the effort to understand. The questioning dominates the activities
of our mind, our drawing of diagrams, our exploring of analogies, our search for
relevant data, our testing of hypotheses. The many disparate activities are
united by the one desire seeking the one solution. Our searching is purposive,
determined.
Archimedes had a desire to know as a mathematician but he had
a strong reinforcement of that desire with the request of the king, the
possibility of a reward and the fear of failure. It became a deep drive in his
psyche, such that, even when he was physically relaxing, somehow unconsciously
he was still working on the problem. Tension is created by the elements that do
not fit together, the clues that we cannot reconcile, the lines and dots that do
not make sense. We cannot tolerate disorder, we do not like a mess, we want to
put things in their place. Puzzles annoy and challenge us. This is the period of
the struggle, the thrashing around, the frustration, as we explore possible
solutions.
When we discover the correct solution we experience it as a
physical, mental and emotional release of tension. The joy of insight is
symbolized by the naked Archimedes rejoicing in the streets of Syracuse. Or
perhaps we can think of Helen Keller, happy for the first time in her life,
eager to begin a new day of learning and insight. It is the joy of a desire that
is satisfied, that has finally reached its goal. It has its emotional side as
frustration, anger, despair give way to joy, contentment, peace in the finding
of the solution. It has an intellectual aspect as the mind too is at peace, the
contradictions have been reconciled, the clues have been put together, we have
hit upon the solution; we cannot comprehend why the others cannot see [68] it.
There is even a physical component to such release; the tension of inquiry can
disturb our sleep, affect our appetite, and interfere with our digestion.
The stream of images, examples, analogies, similar cases,
possibilities that come into our mind are crucial for the generation of
insights. Once we have the right image, clue or example, the insight will follow
very quickly. The stream of images and possibilities come from our imagination
and memory but under the influence of questioning. It is not a random stream. We
dismiss immediately images and examples that have no relevance. The relevant
image, data, example, come readily to mind for the intelligent person.
Concentration means bringing this stream of images under control; distraction
means that the images have taken over and we are being led far from the problem
at hand. Even before insight occurs, intelligent inquiry is active, sorting out
the relevant from the irrelevant, picking out clues, hints, suggestions,
disposing the image so that it can become intelligible. Classical Scholastic
philosophy recognized this activity as disposing or throwing light on the
phantasm preparatory to the act of understanding.
Questioning represents the active aspect of understanding; we
are doing the asking, constructing images, searching for relevant examples. We
can control our imagination and memory and harness them for the purpose of
understanding. Although the particular operations of constructing images and
drawing on examples from memory are activities at the level of sense, they have
been already been harnessed for the work of understanding. Higher animals have
imagination and memory as well as an ability to coordinate responses; but we see
no evidence of an ability to control or construct images. What is missing is
intelligent inquiry; what is distinctively human starts with this inquiry.
You usually profit from a book or course to the extent that
it responds to your personal questions. You will profit from this text to the
extent that you are ceaselessly asking pertinent, critical, personal questions.
What is he at? Is that true? What is the value of that? Surely that is wrong?
How does that fit in here? Philosophy is about asking questions. Sometimes we
think of science and philosophy as providing answers and so they do, but there
are always further [69] questions, different questions, broader and deeper
questions; the questions will always go beyond available answers.
3.2 Insight comes Suddenly and Unexpectedly.
It comes; you cannot force it; you have to wait and hope and
keep trying. But when that moment comes, it is something like a gift, an
intervention from outside, something that happens to us; we receive it, we are
to some extent recipients; we are illuminated. When faced with a problem, we are
active in the sense that we are looking for different images, putting different
bits of information together, searching in the memory for similar examples, etc.
But we are also passive in the sense of waiting, hoping and praying that the
insight will come. Aristotle was on to something when he distinguished between
an Active and Passive Intellect. We need to discriminate between these two
aspects to the act of understanding, the active and the passive.
The act of understanding does not follow automatically after
questioning. In this, we can contrast sensation and understanding. Sensation is
automatic; if you open your eyes you see. If there is light and it is reflected
off surfaces and your eyes are functioning normally, then automatically an image
is cast on the retina and the reactions of the nerve endings send signals to the
brain. If you are shortsighted or long-sighted, wear spectacles and
automatically the image is corrected. If we are not seeing, then something is
wrong with the functioning of the eyes, the nerves or the brain. But
understanding is different. Presented with a puzzle, it does not follow
automatically that you will solve it. Understanding is not like immediate
automatic vision of objects. You cannot impose a timetable; you cannot force an
insight to come; you can only create the conditions in which it is most likely
to occur. Understanding is a highly complicated series of interrelated
operations, in some of which we are active and in others passive.
There is a difference between working out a calculation and
making a discovery. In working out a calculation, you have a problem but you
have clear rules to be followed; if you follow them you will automatically get
the correct result. The process of getting the square root of a number is a
typical example of a calculation. No [70] matter how complicated the number,
simply apply the rules and work out the steps and automatically you will get the
result. But that is because somebody in the beginning figured out what were the
correct rules and procedures to be followed to get the correct result. We learn
the rules, practice how to apply them, and if we follow them we will get the
correct result. Acts of understanding are involved; we understand the rules and
how to apply them but we probably do not understand why these rules get this
result; for that we trust the teacher. But the preliminary exercises we have
suggested at the beginning of the chapter are different because you do not know
what are the rules to apply; they are not calculations but discoveries. You have
to work out which rules to apply; you are on new ground; it is original; there
are no automatic results. Discovery is a new beginning. If there were rules for
discovery the Greeks would have developed the computer. There is intelligence
involved in following rules; but more creative intelligence in discovering what
the rules are in the first place.
To say that insight comes ‘suddenly and unexpectedly’ is
not the same as saying that it comes ‘immediately and easily.’ Sometimes it
can be very difficult and comes only after much research and effort. Whether you
get it or not depends not only on intelligence but also on imagination; an
intelligent person can be lead astray by expecting something more than is there.
There is a certain amount of luck involved in finding the right image,
construction, clue or hint. A certain amount of guesswork is involved in
choosing what seem to be the most fruitful alternatives to follow up. But even
if we stumble on the solution after hours of sleepless work, when it comes, it
still comes suddenly and unexpectedly. Even if we do not notice it, there is
always this aspect of receptivity, passivity, emergence of order from confusion.
It does not always come when we are studying but, as with
Archimedes, it can come when we are relaxing, even when we are walking or
playing or working at something else. If the desire to understand, the tension
of inquiry, is strong enough, then the unconscious seems to continue to work on
the problem and we can wake up in the middle of the night and shout, 'I've got
it.' So it is recommended that when you reach a dead-end in some work, you [71]
take a break, do something else, go for a walk, come back to it later and try
again from a new angle.
3.3 Insights depend on Inner Conditions rather than outer
Circumstances
Even though we cannot force insights to come, we can create
the conditions in which they are more likely to occur. These are mostly inner
conditions in the mind rather than in outer circumstances. Primarily, it means
to be continually asking questions; to be manipulating the data in the direction
we think the solution lies; to be looking at the problem from different angles,
dragging up new images, testing examples, remembering similar situations,
exploring possibilities, trying analogies, starting again when we reach a dead
end.
Students hear the same lecture but receive it in many
different ways. They are in the same classroom, have the same equipment, the
same general educational background; they hear the same words but grasp
different meanings. There is an old Latin tag, Quidquid recipitur, ad modum
recipientis recipitur; whatever is received is received according to the
mode of the recipient. It is the inner conditions of interest, attention,
questions, images, and habits, expectations, ability, which determine how a
lecture is to be received.
The inquiring subject sets the context into which insights
will be received. A person who is familiar with mathematics will easily solve
mathematical problems but may not be so good at crosswords or trick questions.
Someone with a good memory will be good at general knowledge questions but may
have difficulty with math or logic. So much depends on previous education, state
of development of the culture, age, etc. Many people frequented the baths at
Syracuse and experienced the sensation of floating in the water but only one of
them had an insight into the laws of displacement and specific weight. [72]
3.4 An Insight Pivots between the Abstract and the Concrete
On the one hand, an insight is dealing with data and images
which are concrete and particular: Archimedes had one chalice, one King, and one
particular problem to solve. On the other hand, what the insight grasps is an
idea, a relation, a universal, a law; and that is abstract. The laws that
Archimedes eventually formulated were universal, referring not only to this
chalice but also to any other material body immersed in any other liquid at any
time or any place. The insight is constituted precisely by 'seeing' the idea in
the image, the intelligible in the sensible, the universal in the particular,
the abstract in the concrete. We pivot back and forth between images and ideas
as we search for the correct insight. First let us now clarify the difference
between images, ideas and concepts.
3.4.1. Images
An image is a sensible presentation; the most typical kind of
image is the visual image, an imaginary picture. If we imagine a tree, then, it
is a mental picture of a particular tree, with a definite size and shape and
color. Even if we try to neutralize distinguishing features, still, the image
will have a minimum sensible shape and size so long as it is an image. It is the
function of imagination to receive images and to produce images of things that
do not necessarily exist. An image is a product of the imagination. All the
senses give images so there are also tactile images: we can imagine what it
feels like to touch a snake. There are images of hearing: when we write music we
can imagine what it will sound like. We can study a cookery book and imagine
what the different dishes will taste like. We can imagine the smell of freshly
baked bread. All these images are sensible, they are visible or tactile or
audio, images of smell or taste, products of imagination.
We can construct images of things never seen or sensed. We
can combine images such as in a golden mountain or a pink elephant. We can
imagine things that do not exist. We can fantasize about the future. We can do
thought experiments such as imagining what it would be like travelling at half
the speed of light. It is imagination that is imagining, but it is under the
influence or control of intelligence, questioning, searching. But imagination
must first [73] receive the raw material from the senses; a person totally blind
from birth can hardly imagine color.
Animals have imaginations and can store sensible images. Dogs
can be taught to recognize and react to the smell of drugs or explosives or to
follow a trail. Animals remember places and times. But their imaginations are
limited; they do not seem to have free images, to be able to create new images
out of the material received in the senses. The human imagination can do this;
it can construct new combinations of images, extrapolate from images, visualize
new possibilities, write endless fiction. The chess player can look at the board
as it is at the moment but imagine it as it will be after three more moves. This
flexibility is essential for facility in understanding. We can imagine not only
the actual but also the possible, what does not or could not exist.
3.4.2. Ideas
As an image is the content of an act of imagining, so an idea
is the content of an act of understanding. An image is concrete and particular;
an idea is abstract and universal; they are as different as chalk from cheese.
If you take the example of the sequences of numbers given in the exercises you
can see that each number is particular; the next number required is particular.
But the only way to get what generates that number is to grasp the intelligible
relation between the numbers. That is grasped in the formula (e.g. 2x+4); that
is an idea. It is abstract, universal. It can generate an infinity of particular
numbers but by itself it is an abstract, empty formula. Once we have grasped the
idea behind the sequence, we can go forward or backwards as far as we like, but
we quickly find this boring and pointless because it is the same thing over and
over again. An idea is called abstract or universal precisely because in itself
it is not concrete or particular but can be applied to an infinity of concrete
or particular instances. The definition of a circle can be realized in an
infinity of circles of different sizes and colors. The definition of a human
person is a universal but it can be applied to an infinity of particular
cultures, ages, colors, sexes.
There are many different kinds of ideas. We have defined
images as products of imagination and we will define ideas as products of [74]
intelligence. Definitions, laws, relations, intelligibilities, unities,
qualities, quantities, classifications, virtues, numbers, are all ideas. Helen
Keller had an idea when she grasped the connection between the lines traced out
on one hand and the experience of water on the other hand. She grasped a
relation between a word and a reality; this relation is abstract. The lines are
concrete, the water is particular, but she grasped a relation, by which that
word represents that reality. Archimedes grasped a combination of laws operating
on all concrete particular things, the laws of specific weight and flotation.
Poincare grasped the similarity of one branch of mathematics to another. Huffman
grasped the idea of going backwards instead of forwards. There is an almost
infinite variety of different ideas. The crucial point for us at the moment is
to grasp the difference between images, ideas and concepts.
3.4.3. Concepts
Concepts are ideas that are formulated explicitly and
expressed in words or symbols or definitions. A concept is also a product of
conceiving. A direct, simple insight into a particular problem usually comes
first but then we think about it, put it clearly into words and formulate it as
a definition or law. Archimedes had the correct idea of how to proceed when he
was in the baths, but only later defined the concept of specific weight and the
laws of displacement. Ideas come first but are quickly followed by concepts.
Concepts are formulated ideas. Most people have an idea of what constitutes a
circle and would be able to distinguish between a circle, an ellipse and an
ovoid. But many would not be able to define a circle correctly; when you
formulate a definition of a circle explicitly, then, you have the concept of the
circle. Both idea and concept are products of intelligence, not of imagination.
Both concepts and ideas are universal and abstract. It is intelligence that
grasps intelligible relations, meanings, solutions, laws, and expresses them in
a formula or definition. We will discuss this activity of formulating concepts
and definitions in more detail in Chapter five on Developing Understanding and
Formulation.
A concept is only a concept, that is, a creation of the mind
in its purposive search for understanding. We can have strings of concepts [75]
which cluster together to form a theory or explanation. We could invent concepts
at will in the sense of science fiction. But normally concepts are a stage in
the process towards knowledge of the real when we need to be quite clear about
what we are talking about. Concepts are usually a means towards an end, rather
than an end in themselves. Concepts in themselves are simply suppositions. But
they can also be the means by which we understand correctly the working of the
material world. Any technical discipline requires concepts, but they are not the
object of the science in question; they are the means the science uses in order
to know the concrete. Idea and concept, being both products of understanding,
belong very closely together and hence we sometimes use these terms
interchangeably.
The terms 'perception' and 'percept' are used in various
ways: meaning either pure sensation, or full understanding, or anything
in-between. It can be very confusing when people are using the same word in
totally different senses. We would tend to use the word perception to indicate
not a pure sensation, but a sensation that is patterned by understanding.
Psychologists are fond of certain diagrams which challenge our perceptions; a
stairway, which can be perceived as from above or from below; a sketch that can
be either an antelope or a bird - see question five of the preliminary
exercises. For them, these furnish proof that our knowing is subjective; that
the same sensible data can be 'understood' in two different ways depending on
the subjective dispositions of the knower. For us, this is simply an example of
understanding imposing upon or controlling, to some extent, how we see the
diagrams; there is no correct way of seeing such diagrams.
3.4.4. Images and Ideas
The crucial distinction we are making is between images, on
the one hand, and ideas and concepts, on the other. David Hume and many
empiricists after him use the words image and idea in vague and confusing ways.
He defines an idea as a ‘less lively’ image.9
Ideas seem to be vague replicas of vivid images; they have less force but are
the same kind of thing. His intention was to reduce all the contents of the mind
to the level of the sensible. He was trying to say [76] that even the most
abstract ideas could be traced to some image and so could be explained in terms
of the sensible.
We are using the terminology of image and idea in a strictly
defined sense. Ideas are not just less vivid shadows of impressions but have
quite different properties as noticed above. Our appeal for the justification of
this distinction is our own experience of the activity of understanding. What
happens in your mind when you grasp the formula that generates an infinite
sequence? What happened to Archimedes when he grasped the concept of specific
weight? What happened to Newton when he grasped that a line or motion was a
continuum? It is more than imagination. It is intelligence at work. The
imagination produces images. Intelligence produces ideas and concepts. Although
image and idea are clearly distinct they are also closely interrelated in the
process of knowing.
3.4.5. We cannot think without images.
Having distinguished clearly between images and ideas, let us
not make the mistake of separating them. It is a matter of common experience
that we cannot think with out using images. Spontaneously if we are trying to
understand something we appeal to examples, we construct a diagram, we refer to
a particular incident; if we are teaching we similarly use examples, tell
stories, apply metaphors, draw illustrations. By image here we include the vast
store of memories, imaginations and sense data given to us in experiencing.
Insights emerge when we question certain aspects of that data. Ideas emerge from
the images. They are quite distinct from one another. Yet the development of our
understanding continues to depend on appropriate images. It is not as if once we
got the idea we were set free from the senses and imagination. The process of
pivoting between the concrete and the abstract, the image and the idea,
continues.
Images may become more and more rarified but never completely
disappear. The mathematician needs appropriate symbols to facilitate his
procedures. The Romans used an extremely awkward system of mathematical symbols;
it would be extremely difficult to perform operations of multiplication,
division, roots, etc using such symbolism. They had to be replaced by symbols
which [77] were more flexible, more suggestive, more functional. In the
empirical sciences, as we shall see, it is necessary to construct images of
atoms, diagrams of forces and vectors, tables and graphs of data. Even in
theology it would seem very difficult to think of God without some vague image
of light, size, power. In the end we are perhaps left with the image of the word
as the peg on which to hang the idea.
The more appropriate the image the sooner the idea will come;
we need the images to reach the ideas. We have to manipulate, adjust, add to the
images in order to get the insight. Solving problems in Euclidean geometry
usually involves a construction, bisecting an angle, drawing a parallel line,
etc. This is manipulating the image; when we hit on the right construction, we
can usually grasp the solution. There will be much drawing and pencil work in
solving some of the problems at the beginning of this chapter, but the act of
insight that comes at the end produces, not an image, but an idea. It is
intelligence grasping intelligible relations; it is seeing the connection; it is
reaching the definition. Newton's laws of motion are a statement about a series
of interrelated concepts. They are products of insight. The insights would not
have been possible without the experience of motion and the images associated
with the experience, but the insight goes far beyond that experience to grasp
intelligible relations that explains universal qualities of motion. The laws are
universal and abstract. They apply to all motion, of all material bodies,
wherever they may be, past, present and to come, no matter how large or small.
Plato seems to have thought that human intellectual knowing
was a purely spiritual activity not dependent on the senses or images in any
way. To understand was to be able to ‘see’ the intelligible Forms directly
and immediately. For him there was no need for this complicated business of
manipulating images, asking questions, struggling with the data, testing
possibilities, following up leads, and finally getting the point. For Plato
ideas did not emerge; they were already there. It is much simpler to think of
intellectual knowing as a kind of intellectual seeing, simple, single, immediate
contact, but such does not seem to conform to the common experience of the
struggle to understand and the complicated [78] interrelationship of activities
which seem to be necessary for understanding.
David Hume seems to have held the position that human knowing
was simply sensible experience; that ideas are the same sort of thing as images;
that intelligence was the same as imagination. All these ideas and concepts we
have talked about are merely faint images and they are related together because
of certain laws of association. This simplifies matters considerably; we can
eliminate the spiritual, the intellect, metaphysics, theology, and anything else
we don’t like. But the question is, does this square with your understanding
and my understanding as actually experienced in solving a problem or formulating
a universal law? It seems, on the contrary, that human understanding does
involve images and ideas, imagination and intelligence, the concrete and the
abstract, the particular and the universal. It is a complicated process
involving interrelated activities; the attempt to oversimplify simply distorts
rather than clarifies.
Aristotle held the middle position. There is an active
intellect which operates on sensible data to throw light on phantasms to prepare
for the act of understanding.10
Ideas emerge from images; the thinking part, then, thinks the
forms in the images. There is a difference between images and ideas, phantasms
and forms. But they continue to develop together; for this reason the soul never
thinks without images. Aristotle’s account of human understanding is quite
complicated, expressed in difficult metaphysical language, but seems to square
with the actual experience of understanding better than any other theory.
Human knowing combines elements of animal knowing with
intellectual knowing in a new synthesis not just a mixture. It is animal knowing
to the extent that it is tied to the sensible and particular by way of the
external and internal senses. It is intellectual knowing in the sense that the
human intellect can grasp the intelligible, the universal, the necessary, the
abstract, the forms. But human knowing is not just a mixture of these two forms
of knowing; it is a synthesis in which both are involved in a new unity, a new
interrelationship, or interdependence. It is unique; it is complicated. Any
attempt to reduce human knowing to the level of the sensible [79] alone will
fail, because it cannot account for the grasp of the universal. Any attempt to
maintain that human knowing is purely intellectual will fail when we notice the
dependence on the sensible and images. Human knowing involves both images and
ideas, both the concrete and the abstract. It is, perhaps, because it is so
peculiar and so complicated that so many theorists have been tempted to
oversimplify and thus failed to give a comprehensive account of human knowing.
3.5 Insights pass into the habitual texture of the human
mind
If you have solved one of the puzzles at the beginning of the
chapter, it is not easy to forget the solution. Whenever you discover something
for yourself, it is not easily forgotten. There is a great difference between
understanding and memorizing. Something we do not understand is usually very
difficult to memorize; nonsense sequences are the hardest to memorize. But
something we have understood becomes part of our mind in such a way that it is
difficult to forget.
This constitutes the basis for the possibility of learning.
We take it for granted that we can read and do not remember the years of
learning involved in acquiring that skill. Learning the meaning of each letter
was an effort, and when we finally learned it was an act of understanding the
relation between a shape and a sound. Then, we were faced with the further task
of associating letters together to form words. This presupposed the
identification of the individual letters but called for a further step in
associating letters together to form meaningful words. Again, each slow step
forward was an insight, which passed into the habitual texture of the mind.
Finally, there was the challenge of sentences, long sequences of words linked
together to form a meaningful whole. This presupposed the words but went beyond
the words. A new insight was required and when it was attained, then we could
say that we could read. After years it has become so easy that we take it for
granted. But that is only because each of the individual insights have coalesced
and become part of the very texture of our minds.
Much the same thing happens in any area of competence when
the learning process builds up a context of principles, laws and [80] relations,
that are taken for granted as a background when approaching any concrete
problem. A professionally trained mechanic sees and hears the same as the lay
person, but because of his habitual store of principles and theory can attach
significance to data which for the layman is insignificant. Similarly, a doctor,
an astronomer, a physicist, an exegete, a historian, possess a store of theory,
concepts, procedures which has become habitual.
4. Distinguish Experiencing and
Understanding
4.1 Distinct
Our identification of the five characteristics of the
activity of understanding has made us aware of the complexity and subtlety of
this activity. We have started with direct acts of understanding of simple
problems or puzzles. Much remains to be said about developing understanding and
knowing but at least we have made a start on self-appropriation. Now we can
distinguish clearly between two different sets of cognitional operations or
activities, that of experiencing and that of understanding. We will use the
image of levels hoping that it will not be taken too literally; experiencing we
put on the first level and understanding on the second. By experiencing we mean
any activity at the level of the external or internal senses; seeing, hearing,
remembering, imagining, feeling, are all operations of sense. These activities
of the senses we share with the higher animals. They can be explained and
accounted for in terms of animal psychology. In contrast, understanding is a
different kind of activity; it is grasping the intelligible in the sensible, the
abstract in the concrete, the universal in the particular. It is both active and
passive. It involves questioning, struggling, searching for relevant data.
Finally it comes; we grasp the idea, the relation, the law. Experiencing and
understanding are quite dissimilar; it is impossible to just lump them together;
they are distinct activities.
The products of these activities are also distinct; images,
sensations and memories are not the same as ideas and concepts. An image is a
picture or sensible replica of touch or hearing or taste; it is concrete,
sensible, and particular. Our image of a house involves certain dimensions,
colors, and shapes. Without some of those [81] sensible qualities there is no
image. An idea is abstract; the law of specific density states an abstract
relation between weight and volume. To apply the law requires other further
activities; the law itself is an idea, the content of an act of understanding.
Images and ideas are distinct products of the distinct operations of
experiencing and understanding.
Let us explore in what ways these activities are different.
The senses operate immediately on sensible objects. The senses require
direct physical contact between the object seen and the seeing eye. It is
immediate in the sense that there is no intermediary, no other actions involved;
it is direct physical contact. Similarly for the other senses of smelling,
touching, tasting and hearing. Understanding, on the other hand, is mediated
through operations of imagination, memory and questioning. Questions operate on
data to make what is potentially intelligible to become actually intelligible.
Kasparov spent fifty-five minutes on one move; Huffman spent months working on
his problem before he got the simple insight to work backwards instead of
forwards. Why does it take so long to understand? What are we doing before it
comes? Understanding is mediated by questioning, selecting relevant data,
organizing suggestive images, constructing helpful diagrams.
Operations of sense are simple, single activities;
understanding is a complex series of interrelated activities finally
issuing in insight. In experiencing one sense operates on one object, in one
act, and constitutes one seeing or hearing. In contrast, understanding requires
many activities in a sequence to produce one act of understanding. Human
intelligence is discursive, it is a conversation with oneself; it is a jumble of
activities; we rarely go directly to the correct solution; more often we take
many by-ways, make many mistakes, get distracted, come back to it again. We
tried to reconstruct what was going on in Kasparov’s mind for fifty-five
minutes; review your work in writing a paper; the original vague idea, the
research in the library, talking with friends, suggestions of the professor,
preparing notes, writing the first draft, bring order out of chaos. Why does it
take so long to get things clear, to understand? Because it is not one simple,
single activity but a complex series of interrelated activities. [82]
Operations of the senses are passive whereas understanding is
both active and passive. The senses are receptors. The eyes receive light
waves; the ears are designed to receive vibrations; if there is no light there
is no seeing; if there are no vibrations there is no hearing. They are purely
passive; open your eyes and you automatically see what is there to be seen.
Understanding is both active and passive. It is active in the sense of
questioning, manipulating, organizing data, etc; but it is passive in the sense
that when it comes, it comes; it is a reception. There is the aspect of work,
concentration, research, and effort in understanding; but there is also the
aspect of gift. It comes; it is received.
4.2 Not separate
Although these levels of activity are distinct, they are not
separate; they do not normally operate independently of one another. Often if
you claim two things are distinct, it is assumed that they can be physically
separated from one another. We are claiming that experiencing is a distinct
activity from understanding; but understanding cannot occur without the senses.
Let us illustrate some of the many ways by which they are related.
It is possible for a subject to operate at the level of
experience alone at least for a time; there is a sense in which experiencing can
be separate from understanding. We start at the level of sensation, of
experiencing. The child is mostly a bundle of sensations, desires, needs. At
first there is no flicker of intelligence. But the child is seeing, hearing,
tasting and smelling. Activities of experiencing can occur apart from the
operation of understanding.
Understanding presupposes the level of experience. We cannot
ask questions, unless there is some content; there must be something about which
we ask questions. We ask about what we have heard and seen, imagined and
remembered. We do not just understand; we understand something. What is that
something and where does it come from? All the preliminary exercises present
sensible data; the data have to be seen before they are understood. First there
are data that are seen and remembered; initially there is no meaning or sense or
explanation for the phenomena. Later, there follows the moment of seeing the
connection, the meaning, the solution. [83]
However, in a normal adult the sensitive side of us has been
so penetrated and influenced by intelligence that it is quite difficult to
identify a pure sensation, i.e. a sensation that is in no way influenced by
understanding, naming, defining. Compare a cow and a man looking over a fence.
Both have their eyes open, are conscious and seeing in the physical sense. Are
they seeing the same things? The same images are being transferred to the brain
along an optical nerve in much the same way. The cow sees in a physical sense
within the context of its biological pattern of experience and, with its
imagination and memory, can perceive and react to things related to its needs
and instincts; the cow can recognize grass, smell an approaching fox, hear and
fear rumbling thunder in the distance.
The man sees, but he adds identification and naming to his
seeing. He sees five different species of trees; he sees the smoke of the
village in the distance; he sees the lack of nitrogen in the pasture; he sees
one of sheep limping and speculates on the cause. The experience of the adult is
so patterned by organizing intelligence, so shot through with definitions,
identities, relations, so transformed by the influence of insights that have
become habitual, that it is difficult to separate out a sensation that is purely
a biological sensation. It is this synthesis of animal experiencing and emerging
intelligence that constitutes the uniqueness of human knowing.
5. Heuristic Structure
Plato was puzzled that a person, who genuinely asks a
question not knowing the answer, can still recognize the correct answer when it
comes to him. How can he recognize that the answer is correct, if, at first, he
really did not know the answer? This seems to be a contradiction. Either he knew
the answer all along, or he can never find the answer. In the Meno Plato
presents the example of Socrates teaching a slave to solve a geometrical problem
simply by asking questions.11
The problem was to construct a square that would be exactly
twice the area of a given square. The slave had no previous training in
geometry; at the beginning, he genuinely did not know the answer. Socrates asks
a series of rather pointed questions, and by answering them the laborer was able
to discover the solution for [84] himself. He could now recognize that the
answer was correct. What is this mysterious process from not knowing, to
knowing?
One of the major questions in epistemology is, where do our
ideas come from? Roughly speaking, there are three answers. One group says that
we always possessed them, we have innate ideas, we were born with them, they
were always there; these are usually idealists or rationalists. Another group
claims that there are no such thing as ideas, and that what we call ideas are
really less vivid sense images; these would be called empiricists. Then, there
is the Aristotelian tradition, which claims that the human mind produces new
ideas out of images. Let us consider each of these positions in turn.
Plato had to resort to the theory of Reminiscence and Innate
Ideas in order to solve this dilemma. He had to suppose that we already know all
the answers, already have possession of the Forms, from a previous life; but now
that we are embodied, this knowledge has been hindered, buried, has become
unconscious. The learning process is simply the unconscious becoming conscious
on the occasion that the right question is put, or the appropriate teaching is
presented. He had such a high notion of the immutability and infallibility of
intellectual knowing that he could not make it dependent on sense objects which
are always changing.
For the empiricists the difficulty is that if you admit of
truly universal and abstract ideas it is only a short step to admitting a
reality which is beyond sensation. But their position is built on the premise
that there is only sensation and the sensible; therefore, ideas must be the same
as images and these come from sensation.
Our answer, the third position, is that we can generate ideas
out of images. There is a structure in the mind which enables us to move from
images to ideas, from the sensible to the intelligible, from the unknown to the
known. We call it a heuristic structure. 'Heuristic' comes from the same Greek
verb which Archimedes used in his exclamation of joy at his insight, 'Eureka,' I
have found it. A heuristic is a device that helps us to find something, to move
from the unknown to the known; it gives direction to our search. It is an
anticipation of the known while it is still unknown. What is this heuristic?
[85]
At the most general level, we have already identified the
activities of experiencing, questioning and understanding. We can do
self-appropriation and recognize in ourselves the process from images to ideas,
from not knowing to knowing. We can recognize a direction, a movement, a method
in the unfolding of knowing. We have recognized many different mental activities
going on in the mind, when we are understanding and particularly emphasized the
three categories of activities, which we have called questioning, experiencing
and understanding. These are not random activities. The first manifestation of
intelligence is in the purposiveness of asking questions. But questions have to
have a content, are directed at some data given in experience. The aim of the
question is understanding; that is reached when we have the experience of
insight. Is there a method to guide us from the question to the answer? In the
most general sense we can answer yes; it is not a set of rules but general
guidelines which orientate our search. We have identified many different mental
activities going on in the mind when we are understanding. We can distinguish
striving, remembering, writing, drawing, imagining, feeling, following clues,
exploring, separating, rejecting, trying again, giving up, etc. But these are
not random activities. There is a basic method in our madness, there is a
direction in which we are moving.
The unknown is never completely unknown. We can ask questions
about it so we must know something. A question represents a combination of the
known and the unknown. The more clearly we can formulate our question the nearer
we are to answering it ourselves. The first step would seem to be to give the
unknown a name; naming seems to be the first and simplest kind of insight. We do
not know what it is but at least we can refer to it and talk about it. This
technique is particularly effective in algebra where the standard method is to
let 'x' equal the unknown. But it also occurs in the empirical sciences; instead
of 'x' we tend to use such a term as 'the nature of.' What is the nature of
fire? What is the nature of a free fall? What is the nature of AIDS? We have a
name but we do not yet know the intelligibility or law to which it refers.
The second step would seem to be to sort out and relate the
knowns and the unknowns. What do we know about the unknown? [86] What do we want
to know? What are the terms of the question? Write down all that you know. Is
there any way that information can be manipulated in order to reach the unknown?
In algebra the technique consists of forming equations; once you have a
sufficient number of equations, combine them and find the value of 'x'. In the
physical sciences it will be more complicated but the same process is at work.
Much is known about AIDS but there are also many unknowns; call conferences to
share what is known, isolate and pin down what needs to be known and how to find
out. Be clear about everything that is known. State as clearly as possible the
unknown that is being sought. Combine that with what is known. Where is the
significant new data to be found? There will be many different techniques for
finding further information; many complicated calculations involved; many
sophisticated instruments to be used. But the guiding heuristic is the same.
This is the period of struggle, of manipulating the data, of waiting for the
insight to come, of creating the conditions in which it is most likely to occur.
The third step is solving the equations, doing the necessary
observations, working out the solution. The example of the addition sum in the
preliminary exercises is a good example where you must write down all that you
know about each letter. Be perfectly clear about what you know and what you don’t
know. You can infer certain conclusions from the laws of addition, i.e. an even
number plus one gives an odd number; any number added to itself gives an even
number.
There are many specific methods proper to each discipline; we
are often taught the rules of how to proceed, for instance, to identify an
unknown chemical substance. Some disciplines will favor deduction, some
induction; some will favor analysis, some synthesis; some will favor
observation, others experiment. The basic heuristic we are identifying underlies
them all. A heuristic guides our questioning of data to a fruitful and correct
understanding. We have seen that this process is not automatic and cannot be the
subject of rules. But there is a direction, a guidance, an orientation that can
promote the emergence of the idea from the image, the insight from the phantasm.
[87]
Algebra is a particularly clear illustration of heuristic
techniques. The basic technique in algebra is to give the unknown a name; let x
equal the required answer. Now that it has a name it can be manipulated. Combine
it with the data given in the question. Imagine you knew the answer, what could
you conclude? Get equations containing x. Solve the equations. If Fred leaves
the house at three o'clock traveling at fifty miles an hour; and Bob leaves the
house at five o'clock traveling at eighty miles an hour in the same direction,
at what time will he overtake Fred? Let x equal the number of hours after three
o'clock that they will be traveling. Fred will be traveling at fifty miles an
hour for x hours and therefore will cover a distance of 50x miles. Bob will be
traveling at eighty miles an hour for (x-2) hours and therefore will cover a
distance of 80(x-2). But they both travel the same distance, therefore 50x =
80(x-2). Solve the equation and get the value of "x".
The great mathematician, G. Polya, specialized in heuristic
techniques for solving mathematical problems.12
He taught mathematics not in terms of rules, but in terms of general
strategies to be implemented to work towards a solution. He formulated his broad
strategy in four maxims. First, understand the problem; analyze what you given
and what you are looking for; be clear, write it down. Secondly, use experience
from related problems to devise an attack; techniques which worked elsewhere
might work here; identify similar problems; remember previous successes and
failures. Thirdly, carry out the attack. Apply the techniques, do the
calculations, work out the equations, find the coefficients, differentiate,
integrate, etc. Fourthly, ask yourself whether you really believe your answer.
Check backwards, verify, look for mistakes, and search for loopholes. This is
the bare bones of a heuristic which need not be confined to mathematics.
Empirical scientists use the same technique even though they
may not be aware of it. Galileo was searching for the nature of the free fall.
What were the mathematical relations that pinned down the nature of a free fall?
Well, set up an experiment to find out. Chart the series of results of the
experiments. Get the insight that satisfies all the relevant data. Check the
insight back against the data; repeat the experiments. [88]
There is a general heuristic involved once we start asking
questions; the question suggests the direction in which to look for images,
data, further information; the question sets the criteria that decide whether it
has been answered correctly. There is often a scissors-like movement in the
unfolding of understanding. On the one hand, we may be helped by more and better
data, so we look up encyclopaedias, perform experiments, observe more closely.
On the other hand, we need hypotheses, ideas, possibilities; we have to think as
well as look for more data. At some moment the hypothesis fits the data and we
have it.
Let us note, then, that there is a method implicit in these
activities of questioning, experiencing, and understanding. There is the
questioning, the initial puzzlement, the grasping of the problem, the challenge
to understanding, the unrest of an unanswered question. This sets off a
striving, a determination, and a stream of activities aimed at a solution. Our
external senses are involved in looking at the book or blackboard, hearing the
challenge, writing it down on a piece of paper, and beginning to draw lines,
fill in spaces, doodle. Our memory is involved as we try to remember similar
examples, similar problems, analogous puzzles, previous experience of dealing
with this type of challenge. Our imagination is involved as we try to manipulate
the data, construct better diagrams, write down all we know, dissect the
question to sort out the knowns and the unknowns, imagine possibilities.
Finally, hopefully, comes understanding, the breakthrough; things fall together,
the excitement of seeing the point. But that is not the end, as there remains
the task of formulating the insight and checking the solution against the data
or against the criteria set by the question.
It seems then that our minds are dynamic, the source of new
ideas, concepts and theories and that these are derived from the matter of
sensation. The mind is a heuristic structure by which it can proceed from the
unknown to the known, from images to ideas, from the vague to the precise. The
dynamic aspect is represented by questioning which points us in a direction,
sniffs out clues, suggests possibilities and finally hits on the solution. There
is a general method implicit in the very structure of human understanding. We
can work out solutions for ourselves; we do not have to wait to be [89] told; we
do not need to appeal to the Authority of Aristotle or anybody else; we can
recognize when we are right and we can learn from our mistakes.
We reject Plato’s innate ideas and reminiscence because it
does not seem to conform to what actually happens. Why should we be obliged to
call upon such unlikely and complicated presuppositions to account for the
activity of understanding? Intellect does work in tandem with sense and ideas do
emerge from images. We disagree with the empiricist position that ideas are the
same as images. A little self-appropriation seems to indicate that they are
quite different. Our position, then, is that human knowing can be progressive
and cumulative. We can start with primitive insights into data; we continue to
differentiate and develop as our education makes possible; there is no end to
the cyclical development of questioning, sensing, observing, understanding,
reflecting and, finally, knowing.
How then do we recognize an answer as correct if at first we
did not know the answer? The question sets the criteria which must be satisfied
if the answer is to be correct. You recognize that it is correct precisely
because it satisfies these criteria. You check the correctness of the solution
by working backwards to the question to see if it is satisfied. There is a
closing off between the question and the answer. This checking procedure and
other aspects will be explored in detail later when we deal with reflective
insight.
In conclusion, then, this is our description of the
experience of having an individual insight. We have started the work of
intellectual self-appropriation. Already, I hope we have made important
discoveries about the working of the human mind, of your mind. It is just a
beginning and there is much more to be explored. It is enough for the moment
that we recognize this activity as it occurs in our own consciousness; it is
enough that we focus our awareness on this activity to see how it unfolds over
time. It is an activity in which we are constantly engaged. It is the activity
of grasping sense from nonsense; separating what is important from what is
unimportant; distinguishing the essential from the non-essential; picking out
the relevant and leaving behind the irrelevant; focusing on the significant and
ignoring the insignificant. It is intelligence [90] that enables us to do these
mental activities. The intelligent person does them easily, quickly,
expeditiously. The unintelligent person does them with great difficulty, great
effort and often with numerous errors.
Comments on Exercises.
(1) One straightaway assumes that the 'tail' of the fish will
become the new 'head'. But it doesn't take long to see that that does not work.
You have to force your imagination to consider other possibilities. Then it
becomes easy.
(2) Looks deceptively simple but it doesn't seem to work.
Understand the rules correctly: no going over lines once they are drawn; lines
must be drawn continuously. It's impossible. We usually presume we must stay
within the 'box' of points; but nobody said that the lines must remain within
those parameters. Then it becomes reasonably easy.
(3) This necessitates a series of insights. Very clear
diagrams are necessary to distinguish what you know for certain and what you are
experimenting with. Write down everything you know clearly. The key insight is
the peculiarity of the fifth vertical line: how can you add E to O and still get
O? What number can you add to another number to leave it unchanged? (Don’t get
confused between the letter O and the number zero.) At a certain point you may
have to switch from deducing, to assuming something and trying it out
(4) (a) The answer is 35. The formula generating an infinity
of numbers is (x + 10).
(b) The answer is -5. The formula is (x - 4).
(c) The answer is 16. The formula is (X x -2).
(d) This is more difficult as it combines both
multiplication and addition. The answer is 79. Two formulas generate this
sequence, (3x + 4) where x represents the value of the previous number in the
sequence; or (3n - 2) where n is the number of the term in the
sequence.
(5) You might be able to shift from one perspective to
another.
(6) Even though we are understanding all the time, it is
quite difficult to isolate one act of insight and identify its characteristics
and genesis. But it is important to find your own examples in your own
experience. The more detail you can provide the better.
1. Insight,
347.
2.
There is nothing sacred about these examples; you may find other examples of
insight more helpful. Puzzles, games,I.Q. questions, crosswords do provide
examples of simple, clear, single insights.
3.
Quoted from one of his lectures in J. Hadamard, The Psychology of Invention
(New York: Dover,1945), 13.
4.
Helen Keller, The Story of My Life, (New York: Doubleday, 1902), 36.
5.
Scientific American
"Profile: David A. Huffman." Sept 1991, 54.
6.
E.D. Hutchinson, "Varieties of Insight in Humans," "Period of
Frustration in Creative Endeavor," "The Nature of Insight," in
Patrick Mullahy(Ed) A Study of Interpersonal Relations: New Contributions to
Psychiatry, (New York: Grove Press, 1949), 386-445.
7.
See the books of Pierre Angers and Colette Bouchard in bibliography. They use
the method of discovery as a basic educational principle.
8. Insight,
27-31.
9.
David Hume, An Enquiry Concerning Human Understanding, Ed. Charles
W. Hendel, (London: Macmillan, 1955) Section Two, Of the Origin of Ideas..
10.
Aristotle, On the Soul, Ed Hippocrates G. Apostle, (Grinnell, The
Peripathetic Press, 1981), 429a to 432a.
11.
See Ernan McMullin "Insight and the Meno", in Continuum Vol 2
No 3 Autumn 1964, 369-376.
12.
G. Polya, How to Solve it: A New Aspect of Mathematical Method,
(Princetown University Press, 1945).
|